“The Fibonacci Sequence turns out to be the key to understanding how nature designs... and is...
a part of the same ubiquitous music of the spheres that builds harmony into atoms, molecules,
crystals, shells, suns and galaxies and makes the Universe sing.”
― Guy Murchie, The Seven Mysteries of Life: An Exploration of Science and Philosophy
Fibonacci in Art and Music
Let's take a closer look at the Fibonacci Sequence we have created: 0, 1, 1, 2, 3, 5, 8, 13, etc.
The next number in the sequence is found by adding up the two numbers before it.
If we pick one number and divide it by the previous number, the ratio of the pair gets closer and closer to 1.618 as we move to bigger numbers. This is what some people call "The Divine Proportion" or "The Golden Ratio".
Da Vinci's Mona Lisa
When you make squares out of those values from the Fibonacci Sequence, it makes a nice-looking spiral. This sequence, pattern, and spiral crop up in many things you might have never noticed. Leonardo da Vinci, who illustrated the aforementioned book, called the ratio the sectio aurea (golden section). Take a look at how da Vinci employed it in one of his most famous paintings, the Mona Lisa.
Musical Instruments
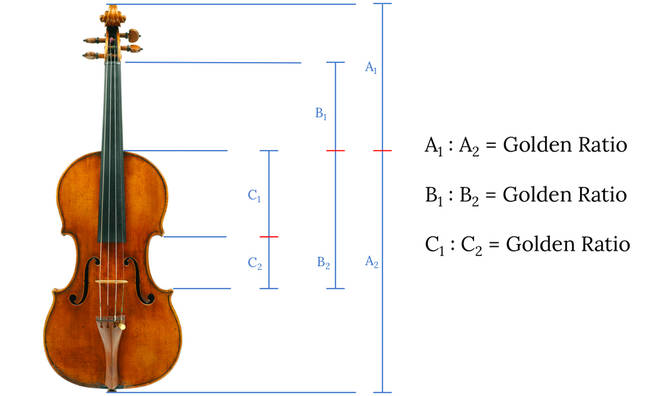
Hailed as the master of violin making, Antonio Stradivari has made some of the most
beautiful and sonorous violins in existence. A Stradivarius violin remains one of the
most expensive musical instruments even after hundreds of years. Its supreme sound
quality may partly be affected by the Fibonacci Sequence and its Golden Ratio measured
by dividing lengths of specific parts of the violin.
Aside from being applied to make violins, the Golden Ratio that comes from the Fibonacci
Sequence is also used for certain saxophone mouthpieces, in speaker wires, and even in
the
acoustic design of some cathedrals.
Music Theory
- The Fibonacci Sequence plays a big part in Western harmony and musical scales. Here are
some patterns:
- An octave on the piano consists of thirteen notes. Eight are white keys and five are black keys.
- A scale is composed of eight notes, of which the third and fifth notes create the foundation of a basic major triad chord.
- In a scale, the dominant note is the fifth note, which is also the eighth note of all 13 notes that make up the octave. Eight divided by 13 equals 0.61538 - the approximate Golden Ratio
Starting to see a pattern? These are all numbers in the Fibonacci Sequence: 3, 5, 8, 13.
Beethoven 5
In 1978, Derek Haylock argued about the presence of the golden section in the first movement of Beethoven’s Symphony No. 5. Claiming that the opening three-note motive and its main theme returns in the original key at the golden mean point of 0.618, namely in bar 372 of 601. What’s more, the coda is 129 bars long, and, if you divide it using the golden section, you get 49:80. After the first 49 bars of the coda, Beethoven actually introduces a completely new tune that has not appeared in the movement so far, a real first in the history of classical music composition.
Golden Ratio + Gaga
Lady Gaga's "Perfect Illusion" features an extremely bold key change right at the 111-second point (1:51). But what’s so great about that?
111 X 1.618 = 179.598
The Golden Ratio! By putting the key modulation at 111 out of 179 seconds, Lady Gaga has found the sweet spot - 1 : 1.618. In a similar way how Beethoven uses Golden Ratio to structure his Symphony No. 5, the high point of "Perfect Illusion" seems to fall at the point that is related to the Golden Ratio.Media Disclaimer
No copyright infringement intended. All copyrights of the graphic and video content belong to the original artists and publishing companies. Under no circumstances will Zhang be responsible or liable in anyway fo any media content presented on Fibonacci Musicale.
